SI病毒模型解析及模拟

由
文章索引 显示

解析

把人群分为两种，一种是易感者，即健康人群，用 S 表示其人数。
另外一种为感染者，用 I 来表示。
即区域内总人数是N=S+I。
I 个感染者，每天碰到 r个人，\( \beta\) 概率会传染疾病。
健康人占比为\( \frac{S}{N}\)。
易得将以上所有量相乘即每天新增感染病例。
于是得到

常微分方程

\( \frac{dI}{dt}=r\beta I\frac{S}{N} \\ \frac{dS}{dt}=-r\beta I\frac{S}{N}\)

现假设总人数N=100，感染者接触易感者的人数r=2，传染概率\(\beta\)=0.02，初始感染者为1即\( I\left(0\right)=1\)。

解

\( I\left(t\right)=\frac{100}{e^{\mathrm{ln}\left(99\right)-\frac{t}{25}} +1} \\ S\left(t\right)=\frac{100}{e^{\frac{t}{25}-\mathrm{ln}\left(99\right)} +1}\)

为观察其变化率对其求导，得

导数

\( \frac{\mathrm{d}}{\textrm{d}t}I=\frac{4e^{\mathrm{ln}\left(99\right)-\frac{t}{25}} }{{\left(e^{\mathrm{ln}\left(99\right)-\frac{t}{25}} +1\right)}^2 } \\ \frac{\mathrm{d}}{\mathrm{d}t}S=-\frac{4e^{\frac{t}{25}-\mathrm{ln}\left(99\right)} }{{\left(e^{\frac{t}{25}-\mathrm{ln}\left(99\right)} +1\right)}^2 }\)

为找出增长速度最快的时间，求其导数最大值，即

最快增长时间

\(t={I^{\prime } \left(t\right)}_{\mathrm{max}} =25\,\mathrm{log}\left(99\right)\approx 115\)

代入原方程发现此时N=50，其实可以通过简单变换直接得出最快增长时间。
\(\frac{dI}{dt}=r\beta I\frac{S}{N}=r\beta I\frac{N-I}{N}=r\beta I\left(1-\frac{I}{N}\right)\)，所以当\(I=\frac{N}{2}\)时增长最快。

为分析何时所有人被感染，故解导函数等于零（实际上该数学模型永不为0，这里以\( {10}^{-3}\)代替），得

全部被感染时间

\(t=25\,\mathrm{log}\left(99\right)-25\,\mathrm{log}\left(1999-60\,\sqrt{10}\,\sqrt{111}\right)\approx 322\)

图解

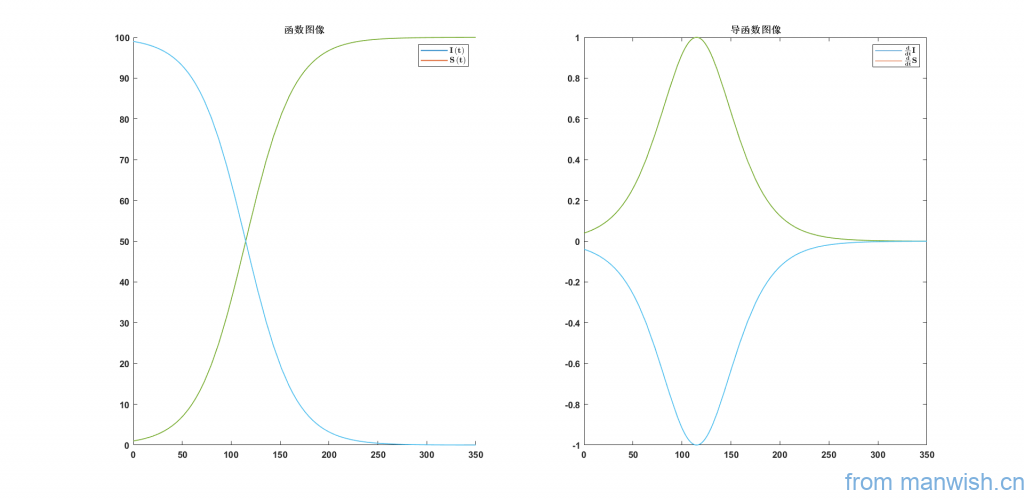
通解

解析解

\( I\left(t\right)=\frac{N}{e^{\mathrm{ln}\left(-\frac{I_0 -N}{I_0 }\right)-\beta \;r\;t} +1} \\ S\left(t\right)=\frac{N}{e^{\mathrm{ln}\left(-\frac{I_0 }{I_0 -N}\right)+\beta \;r\;t} +1}\)

导数

\( \frac{\mathrm{d}}{\textrm{d}t}I=\frac{N\,\beta \,r\,{\mathrm{e}}^{\mathrm{log}\left(-\frac{I_0 -N}{I_0 }\right)-\beta \,r\,t} }{{{\left({\mathrm{e}}^{\mathrm{log}\left(-\frac{I_0 -N}{I_0 }\right)-\beta \,r\,t} +1\right)}}^2 } \\ \frac{\mathrm{d}}{\textrm{d}t}S=-\frac{N\,\beta \,r\,{\mathrm{e}}^{\mathrm{log}\left(\frac{N-S_0 }{S_0 }\right)+\beta \,r\,t} }{{{\left({\mathrm{e}}^{\mathrm{log}\left(\frac{N-S_0 }{S_0 }\right)+\beta \,r\,t} +1\right)}}^2 }\)

增长速率最快时间

\( t=\frac{\mathrm{log}\left(-\frac{I_0 -N}{I_0 }\right)}{\beta \,r}\)

全部被感染时间

取\(0={10}^{-3}\)

\(t=\frac{\mathrm{log}\left(-\frac{I_0 -N}{I_0 }\right)-\mathrm{log}\left(500\,N\,\beta \,r-500\,N\,\beta \,r\,\sqrt{\frac{250\,N\,\beta \,r-1}{250\,N\,\beta \,r}}-1\right)+2\,\pi \,k\,\mathrm{i}}{\beta \,r} \)

\( \left( \begin{align}
& {{\sigma }_{1}}\ne 1\wedge 500\,N\,\beta \,r\ne {{\sigma }_{2}}+1\wedge N\ne 0\wedge \beta \ne 0 \\
& \wedge r\ne 0\wedge {{\text{e}}^{\log \left( 500\,N\,\beta \,r-{{\sigma }_{2}}-1 \right)-2\,\pi \,k\,\text{i}}}\ne -1\wedge k\in \mathbb{Z} \\
& \text{其中} \\
& {{\sigma }_{1}}=500\,N\,\beta \,r+{{\sigma }_{2}} \\
& {{\sigma }_{2}}=500\,N\,\beta \,r\,\sqrt{\frac{250\,N\,\beta \,r-1}{250\,N\,\beta \,r}} \\
\end{align} \right)\)

查看所有模型及注解：点击病毒传染的动态扩散模拟及数学模型

网络模拟

图示

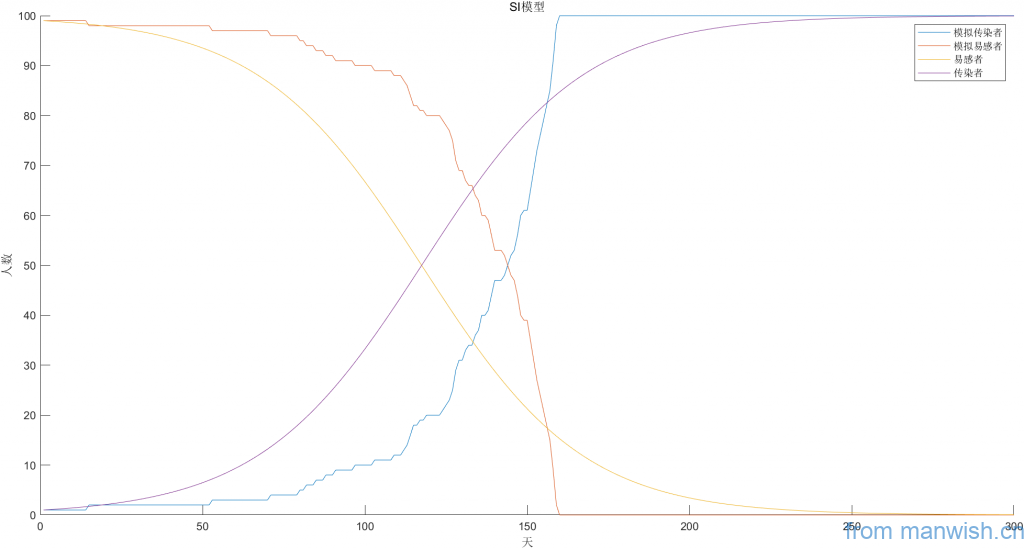
Matlab代码

clear
figure
N = 100;    %初始化图点数
I = 1;      %传染者
Start = 20; %起始点
r = 2;      %感染者接触易感者的人数
B = 0.02;   %传染概率
days = 300;

A=zeros(N);
Ae1=linspace(1,N,N);
Ae2=randi([1 N],1,N);
Ae3=randi([1 N],1,N);
G = graph(A);
G = addedge(G,Ae1,Ae2,1);
G = addedge(G,Ae1,Ae3,1);

[bin,binsize] = conncomp(G);
idx = binsize(bin) == max(binsize);
G = subgraph(G, idx);

G = simplify(G);
Lsg=max(binsize);
S=Lsg-I;    %未感染者

xp=randi([0,N],1,Lsg);
yp=randi([0,N],1,Lsg);
zp=randi([0,N],1,Lsg);
p=plot(G,'Layout','force3',"NodeLabel",[]);
%p=plot(G,'XData',xp,'YData',yp,'ZData',zp,"NodeLabel",[]);
%axis([0 N 0 N 0 N])
p.NodeColor="g";
hold on

Ig = Start;
DATA=repelem(Lsg,days);
DATA(1)=I;
highlight(p,Ig,"NodeColor","red");
title('第1天')
%gif('SI-Graph.gif')
StopDay=0;
for DAY=2:days
    if length(Ig)==Lsg
        if StopDay==DAY
            break
        end
        if StopDay==0
            StopDay=DAY+30;
        end
    end
    for i=1:length(Ig)
        BFS=bfsearch(G,Ig(i));
        BFS=setdiff(BFS,Ig,'stable');
        if r>length(BFS)
            front=length(BFS);
        else
            front=r;
        end
        BFS=BFS(1:front)';
        for lp=1:front
            if rand()<=B
                Ig = [Ig BFS(lp)];
                highlight(p,BFS(lp),"NodeColor","red");
            end
        end
    end
    title(['第' num2str(DAY) '天'])
    DATA(DAY)=length(Ig);
    if rem(DAY,2)==0
        %[caz,cel] = view;
        %view(caz+1,cel)
        drawnow
        %gif
    end
end

figure
N=Lsg;
hold on
xp=linspace(1,length(DATA),length(DATA));
plot(xp,DATA,xp,Lsg-DATA)
T = 1:days;
for idx = 1:length(T)-1
    if S(idx)<0
        S(idx)=0;
    end
    if I(idx)>N
        I(idx)=N;
    end
    S(idx+1) = S(idx) - r*B*I(idx)*S(idx)/N;
    I(idx+1) = I(idx) + r*B*I(idx)*S(idx)/N;
end
a=plot(T,S,T,I);
legend('模拟传染者','模拟易感者','易感者','传染者');
xlabel('天');ylabel('人数')
title('SI模型')Code language: Matlab (matlab)

笛卡尔坐标系模拟

图示(动态过程未给出)

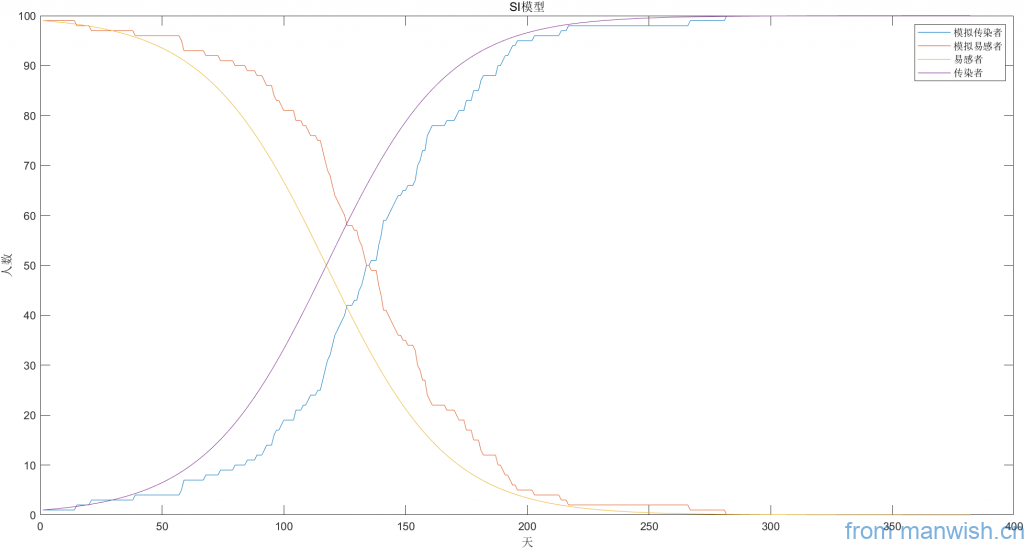
Matlab代码

clear
figure
N = 100;    %人口总数
I = 1;      %传染者
S = N - I;  %易感者

R = 2;      %感染者接触易感者的人数
B = 0.02;   %传染概率
days = 400;
Dynamic = false;  %设置为true显示动态模拟过程

Sdata=[];

state=zeros(1,N);
index=randperm(N,I);
state(index)=1;
if Dynamic
    axis([0 N 0 N]);
    hold on
end
for i=1:days
    xpos=randperm(N);
    ypos=randperm(N);
    if sum(state)==100
        break
    end
    for j=1:N
        if state(j)~=1
            continue
        end
        dis=sqrt((xpos-xpos(j)).^2+(ypos-ypos(j)).^2);
        l=0;
        for k=1:N
            if state(k)==1
                continue
            end
            l=l+1;
            peo(l).dis=dis(k);
            peo(l).num=k;
        end
        T = struct2table(peo);
        sortedT = sortrows(T,'dis');
        sortedS = table2struct(sortedT);
        tp=sortedT{1:R,2};
        for k=1:length(tp)
            if rand()<=B
                state(tp(k))=1;
            end
        end
    end
    Sdata(i)=sum(state);
    a=-8;
    b=8;
    %xpos=xpos+ a + (b-a).*rand(1,N);
    %ypos=ypos+ a + (b-a).*rand(1,N);
    if Dynamic && rem(i,10)==0
        phd=scatter(xpos,ypos,[],state,"filled");
        title(['第' num2str(i) '天'])
        drawnow
        delete(phd)
    end
end

figure
set(gcf,'visible',true)
days=length(Sdata);
plot(1:days,Sdata,1:days,N-Sdata)
hold on
T = 1:days+100;
for idx = 1:length(T)-1
    if S(idx)<0
        S(idx)=0;
    end
    if I(idx)>N
        I(idx)=N;
    end
    S(idx+1) = S(idx) - R*B*I(idx)*S(idx)/N;
    I(idx+1) = I(idx) + R*B*I(idx)*S(idx)/N;
end
plot(T,S,T,I);
legend('模拟传染者','模拟易感者','易感者','传染者');
xlabel('天');ylabel('人数')
title('SI模型')Code language: Matlab (matlab)

留下评论