引言
传染病的数学模型可以预测传染病如何发展,以显示流行病的可能结果,并有助于为公共卫生干预提供依据。模型使用基本假设或统计数据以及数学来找到各种传染病的参数,并使用这些参数来计算各种干预措施(例如大规模疫苗接种计划)的效果。建模可以帮助确定要避免的干预措施和进行试验的方法,或者可以预测未来的增长模式等。[1]
使用Matlab进行模拟和绘图
模拟包括网络模拟和平面坐标系模拟
首页仅提供基本信息等,欲查看详细请点击每个模型的详细解析及Matlab代码
使用Matlab代码前,有问题请先查看注解,代码编写及运行平台为MatlabR2019b。
SI模型:
把人群分为两种,一种是易感者,即健康人群,用 S 表示其人数。
另外一种为感染者,用 I 来表示。
即区域内总人数是N=S+I。
I 个感染者,每天碰到 r个人,\( \beta\) 概率会传染疾病。
健康人比例为\( \frac{S}{N}\)。
将以上所有量相乘即每天新增感染病例。
详细解析及Matlab代码
微分方程
\( \frac{dI}{dt}=r\beta I\frac{S}{N} \\ \frac{dS}{dt}=-r\beta I\frac{S}{N}\)
迭代方程
\(I_n =I_{n-1} +r\beta I_{n-1} \frac{S_{n-1} }{N} \\ S_n =S_{n-1} -r\beta I_{n-1} \frac{S_{n-1} }{N} \)
模拟及理论趋势图
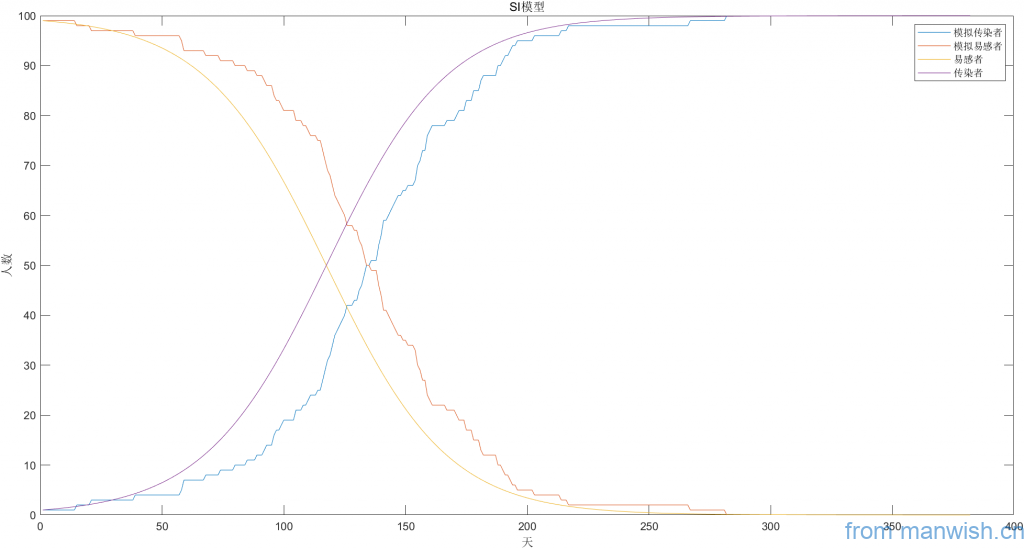
SIS模型:
增加感染者 I 恢复健康的概率\(\gamma\)。
恢复后仍有可能被再次感染。
详细解析及Matlab代码
微分方程
\( \frac{\mathrm{d}}{\mathrm{d}t}I=r\beta I\frac{S}{N}-\gamma I \\ \frac{\mathrm{d}}{\mathrm{d}t}S=-r\beta I\frac{S}{N}+\gamma I\)
迭代方程
\( I_n =I_{n-1} +r\beta I_{n-1} \frac{S_{n-1} }{N}-\gamma I_{n-1} \\ S_n =S_{n-1} -r\beta I_{n-1} \frac{S_{n-1} }{N}+\gamma I_{n-1}\)
模拟及理论趋势图
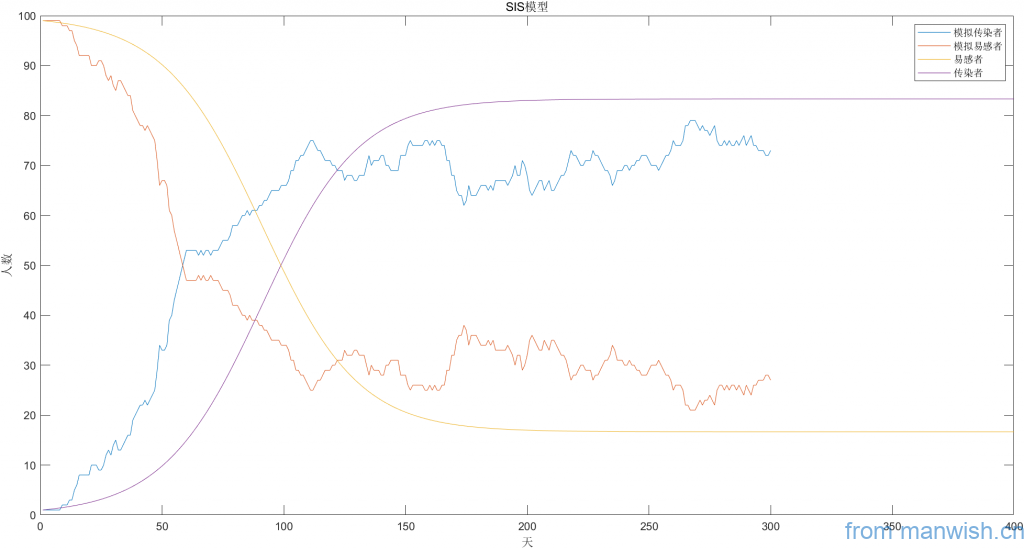
SIR模型:
引入康复者 R ,并满足总人数 N=S+I+R 。
一旦变为康复者,就没有概率再次变为感染者或者易感者。
实际上是将SIS模型中\( \frac{d}{\textrm{d}t}S\)中\( \gamma I\)拿出来,赋值新微分\( \frac{d}{\textrm{d}t}R\)
微分方程
\( \frac{\mathrm{d}}{\mathrm{d}t}I=r\beta I\frac{S}{N}-\gamma I \\ \frac{\mathrm{d}}{\mathrm{d}t}S=-r\beta I\frac{S}{N} \\ \frac{\mathrm{d}}{\mathrm{d}t}R=\gamma I\)
迭代方程
\(I_n =I_{n-1} +r\beta I_{n-1} \frac{S_{n-1} }{N}-\gamma I_{n-1} \\ S_n =S_{n-1} -r\beta I_{n-1} \frac{S_{n-1} }{N} \\ R_n =R_{n-1} +\gamma I_{n-1}\)
模拟及理论趋势图
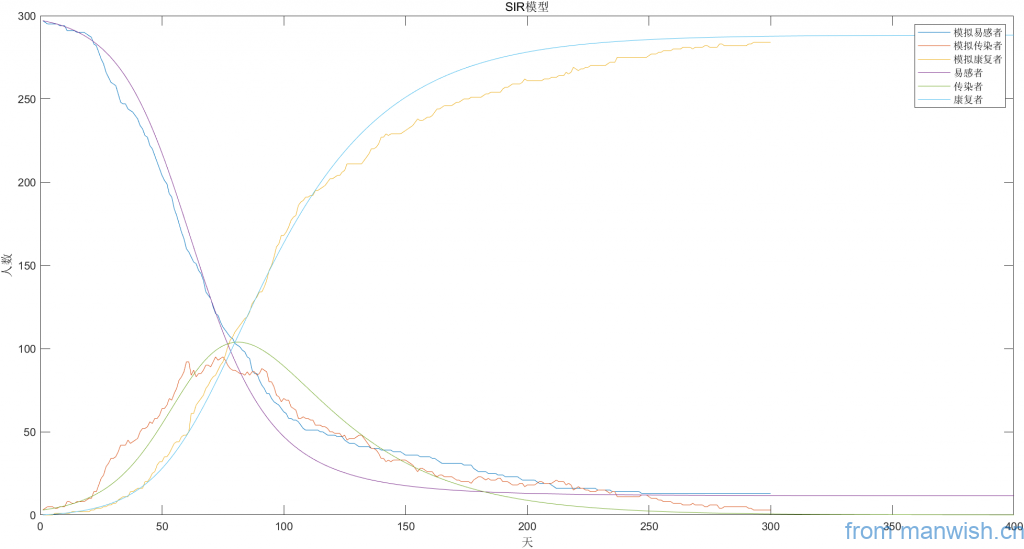
Matlab代码
SEIR模型:
易感染人群在一开始会经历潜伏期,一段时间之后才出现症状。
因此在SIR模型的基础上引入潜伏者E,潜伏者按照概率\( \alpha\)转化为感染者
将SIR模型中\( \frac{d}{\textrm{d}t}I\)的\( r\beta I\frac{S}{N}\)交给\( \frac{d}{\textrm{d}t}E\),新增\( \alpha E\)给\( \frac{d}{\textrm{d}t}E\)和\( \frac{d}{\textrm{d}t}I\)。
微分方程
\( \frac{\mathrm{d}}{\mathrm{d}t}E=r\beta I\frac{S}{N}-\alpha E \\ \frac{\mathrm{d}}{\mathrm{d}t}S=-r\beta I\frac{S}{N} \\ \frac{\mathrm{d}}{\mathrm{d}t}R=\gamma I \\\frac{\mathrm{d}}{\mathrm{d}t}I=\alpha E-\gamma I\)
迭代方程
\(I_n =I_{n-1} +\alpha E_{n-1} -\gamma I_{n-1} \\ S_n =S_{n-1} -r\beta I_{n-1} \frac{S_{n-1} }{N} \\ E_n =E_{n-1} +r\beta I_{n-1} \frac{S_{n-1} }{N}-\alpha E_{n-1} \\ R_n =R_{n-1} +\gamma I_{n-1}\)
模拟及理论趋势图
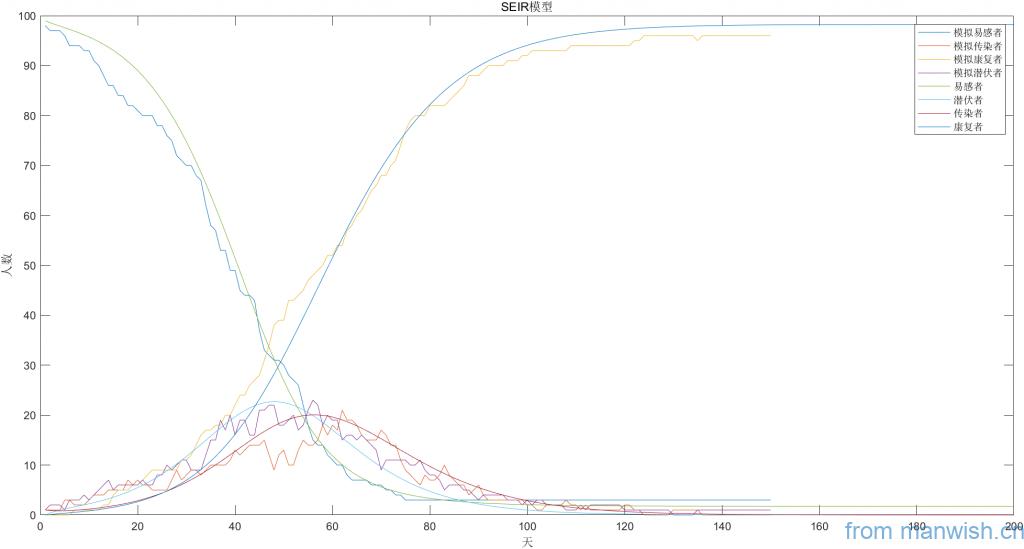
Matlab代码
改进的SEIR模型:
实际上,潜伏者和正常人接触后也可能让正常人变成潜伏者。
因此引入潜伏者的传染概率\(\beta_2\)可以将健康的易感者转变为潜伏者。
潜伏者每天接触的健康易感者人数为\(\gamma_2\)。
引入戒严措施,使得从开始戒严(第D天)后接触人数减少。
微分方程
\( \frac{\mathrm{d}}{\mathrm{d}t}E=r\beta I\frac{S}{N}-\alpha E+r_2 \beta_2 E\frac{S}{N} \\ \frac{\mathrm{d}}{\mathrm{d}t}S=-r\beta I\frac{S}{N}-r_2 \beta_2 E\frac{S}{N} \\ \frac{\mathrm{d}}{\mathrm{d}t}R=\gamma I \\ \frac{\mathrm{d}}{\mathrm{d}t}I=\alpha E-\gamma I\)
迭代方程
\( I_n =I_{n-1} +\alpha E_{n-1} -\gamma I_{n-1} \\ S_n =S_{n-1} -r\beta I_{n-1} \frac{S_{n-1} }{N}-r_2 \beta_2 E_{n-1} \frac{S_{n-1} }{N} \\ E_n =E_{n-1} +r\beta I_{n-1} \frac{S_{n-1} }{N}-\alpha E_{n-1} +r_2 \beta_2 E_{n-1} \frac{S_{n-1} }{N} \\ R_n =R_{n-1} +\gamma I_{n-1}\)
模拟及理论趋势图
未实施隔离措施
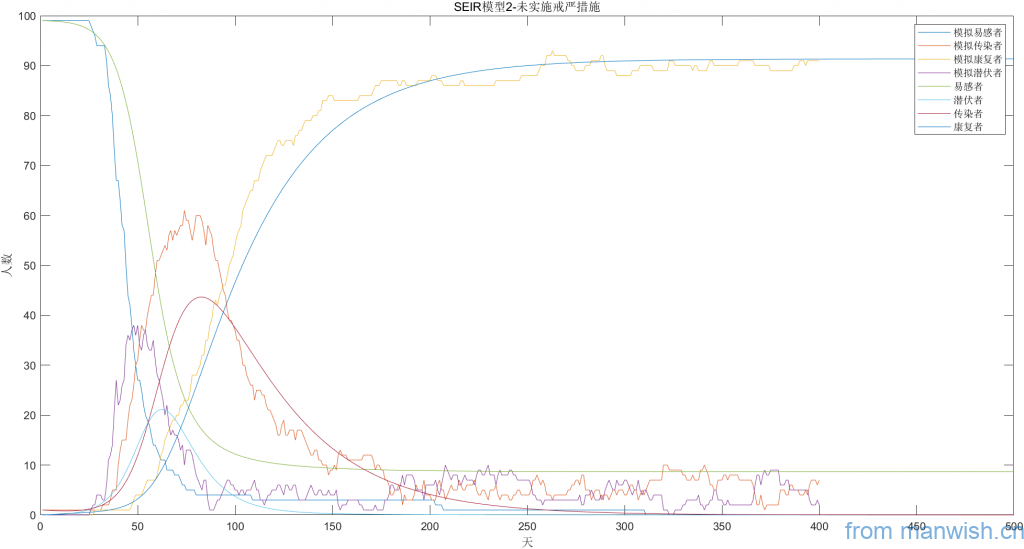
第20天开始实施隔离措施
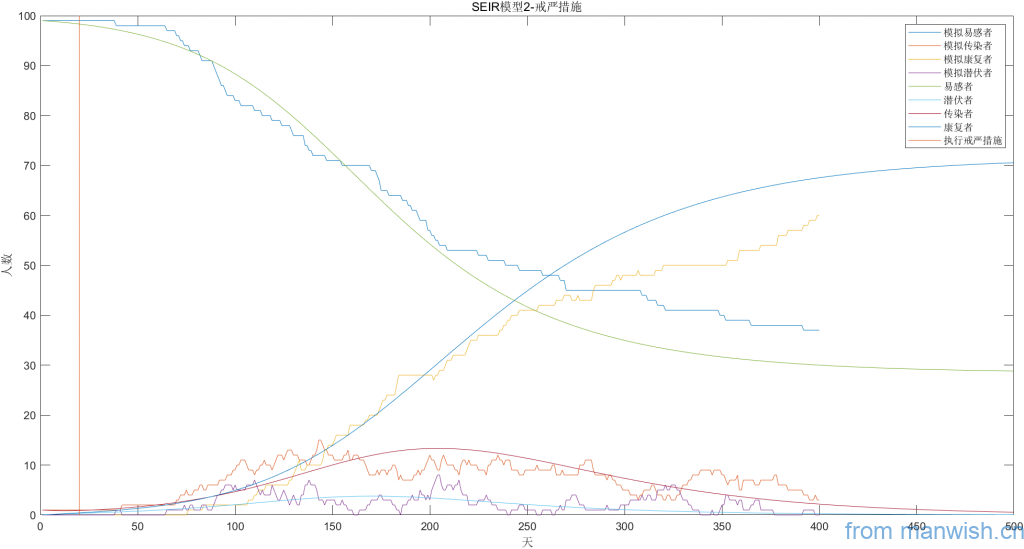
Matlab代码
注解
若有错误烦请不吝赐教。
Matlab模拟代码参数中,感染者起始数量设置为1以加快模拟速度。但这会造成在有康复情况下第一个人直接愈合从而模拟出异常数据,再次运行即可。
对于模拟代码如未特殊说明,那么严格按照微分方程进行模拟。
例如SI模型中感染者每天仅仅会接触易感者r人,将忽略最近的已感染者。
平面模拟完全基于笛卡尔坐标系。
网络模拟基于图,可视化使用三维力导向图布局显示。
网络模拟需要建立强连通简单图,程序在以总人数为N的图中找出节点最多的强连通子图再化简为简单图,故实际人数(变量Lsg)在建图后可能会比预先总人数N少。
如非要在度少的情况下建立大网络请先找出所有连通子图并建立边使其成为桥即可。根据不同情况需要进行适当调整。
稍加更改网络代码就可以模拟出带人际关系的传播,这里不对所有模型进行这种模拟。
网络模拟的速度比笛卡尔坐标系要快。
对于更大的数据,可以执行BFS使其仅找出感染者的前r个人,但这需要手动编写代码。
模拟图中的理论值曲线采用迭代常微分方程方法绘制,解析中理论曲线根据解析解或数值解绘制。
制作中.....
本文标题:传染病模型模拟和理论趋势
本文链接:https://manwish.cn/article/infectious-disease-model-simulation-and-theoretical-trends.html